粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读

2024/08/12

1995年，受到鸟群觅食行为的规律性启发，James Kennedy和Russell Eberhart建立了一个简化算法模型，经过多年改进最终形成了粒子群优化算法(Particle Swarm Optimization, PSO) ，也可称为粒子群算法^[1]。

粒子群算法具有收敛速度快、参数少、算法简单易实现的优点（对高维度优化问题，比遗传算法更快收敛于最优解），但是也会存在陷入局部最优解的问题，enen......

粒子群算法的思想源于对鸟群觅食行为的研究，鸟群通过集体的信息共享使群体找到最优的目的地。如下图，设想这样一个场景：鸟群在森林中随机搜索食物，它们想要找到食物量最多的位置。但是所有的鸟都不知道食物具体在哪个位置，只能感受到食物大概在哪个方向。每只鸟沿着自己判定的方向进行搜索，并在搜索的过程中记录自己曾经找到过食物且量最多的位置，同时所有的鸟都共享自己每一次发现食物的位置以及食物的量，这样鸟群就知道当前在哪个位置食物的量最多。在搜索的过程中每只鸟都会根据自己记忆中食物量最多的位置和当前鸟群记录的食物量最多的位置调整自己接下来搜索的方向。鸟群经过一段时间的搜索后就可以找到森林中哪个位置的食物量最多（全局最优解）。

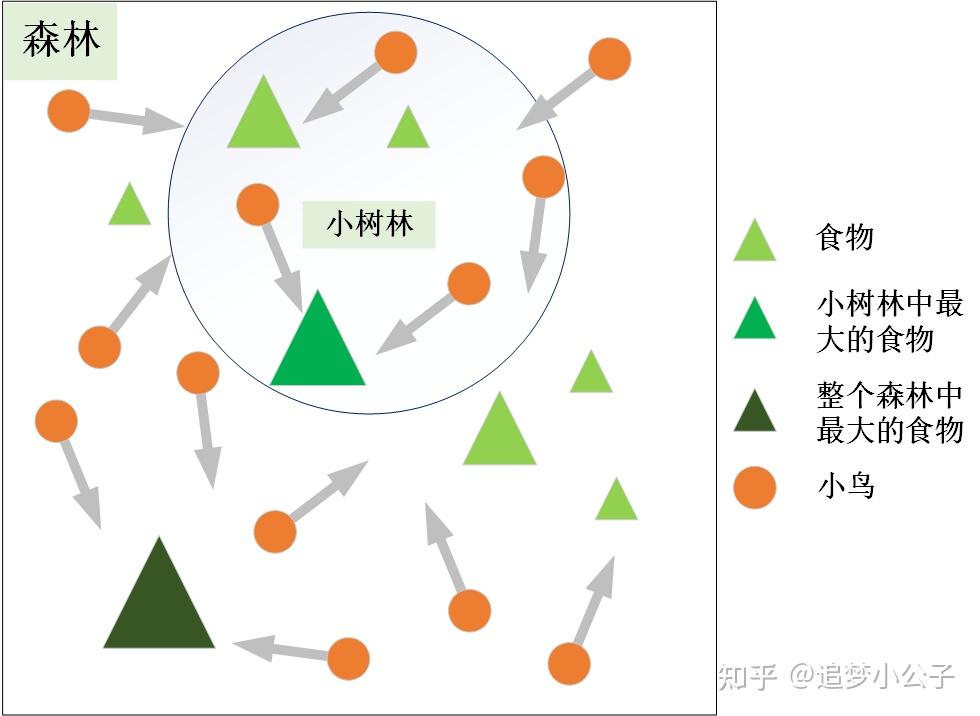
将鸟群觅食行为和算法原理对应，如下图：

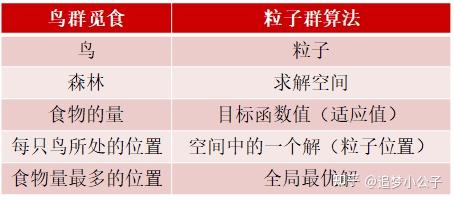
速度表示粒子下一步迭代时移动的方向和距离，位置是所求解问题的一个解。

假设在 $D$ 维搜索空间中，有 $N$ 个粒子，每个粒子代表一个解，则：

① 第 $i$ 个粒子的位置为：

$X_{id}=\\left(x_{i 1}, x_{i 2}, \\ldots, x_{i D}\\right)$

② 第 $i$ 个粒子的速度（粒子移动的距离和方向）为：

$V_{id}=\\left(v_{i 1}, v_{i 2}, \\ldots, v_{i D}\\right)$

③ 第 $i$ 个粒子搜索到的最优位置（个体最优解）为：

$P_{id,pbest}=\\left(p_{i 1}, p_{i 2}, \\ldots, p_{i D}\\right)$

④ 群体搜索到的最优位置（群体最优解）为：

$P_{d,gbest}=\\left(p_{1,gbest}, p_{2,gbest}, \\ldots, p_{D,gbest}\\right)$

⑤ 第 $i$ 个粒子搜索到的最优位置的适应值（优化目标函数的值）为：

$f_p$ ——个体历史最优适应值

⑥ 群体搜索到的最优位置的适应值为：

$f_g$ ——群体历史最优适应值

表述上叫速度，实际上就是粒子下一步迭代移动的距离和方向，也就是一个位置向量。

$\\[v_{id}^{k+1}=\\omega v_{id}^{k}+{{c}_{1}}{{r}_{1}}\\left( p_{id,\ ext{pbest}}^{k}-x_{id}^{k}\\right)+{{c}_{2}}{{r}_{2}}\\left( p_{d\ ext{,gbest}}^{k}-x_{id}^{k}\\right)\\\\\\]$

① 第一项：惯性部分

由惯性权重和粒子自身速度构成，表示粒子对先前自身运动状态的信任。

② 第二项：认知部分

表示粒子本身的思考，即粒子自己经验的部分，可理解为粒子当前位置与自身历史最优位置之间的距离和方向。

③ 第三项：社会部分

表示粒子之间的信息共享与合作，即来源于群体中其他优秀粒子的经验，可理解为粒子当前位置与群体历史最优位置之间的距离和方向。

$N$ ——粒子群规模； $i$ ——粒子序号， $\\[i=1,2,\\ldots ,N\\]$ ；

$D$ ——粒子维度； $d$ ——粒子维度序号， $d=1,2, \\ldots, D$ ；

$k$ ——迭代次数； $\\[\\omega\\]$ ——惯性权重； ${{c}_{1}}$ ——个体学习因子； ${{c}_{2}}$ ——群体学习因子；

${{r}_{1}},{{r}_{2}}$ ——区间 $[0,1]$ 内的随机数，增加搜索的随机性；

$v_{id}^{k}$ ——粒子 $i$ 在第 $k$ 次迭代中第 $d$ 维的速度向量；

$x_{id}^{k}$ ——粒子 $i$ 在第 $k$ 次迭代中第 $d$ 维的位置向量；

$p_{id,\ ext{pbest}}^{k}$ ——粒子 $i$ 在第 $k$ 次迭代中第 $d$ 维的历史最优位置，即在第 $k$ 次迭代后，第 $i$ 个粒子（个体）搜索得到的最优解；

$p_{d\ ext{,gbest}}^{k}$ ——群体在第 $k$ 次迭代中第 $d$ 维的历史最优位置，即在第 $k$ 次迭代后，整个粒子群体中的最优解。

粒子下一步迭代的移动方向=惯性方向 + 个体最优方向 + 群体最优方向

上一步的位置 + 下一步的速度

$\\[x_{id}^{k+1}=x_{id}^{k}+v_{id}^{k+1}\\\\\\]$

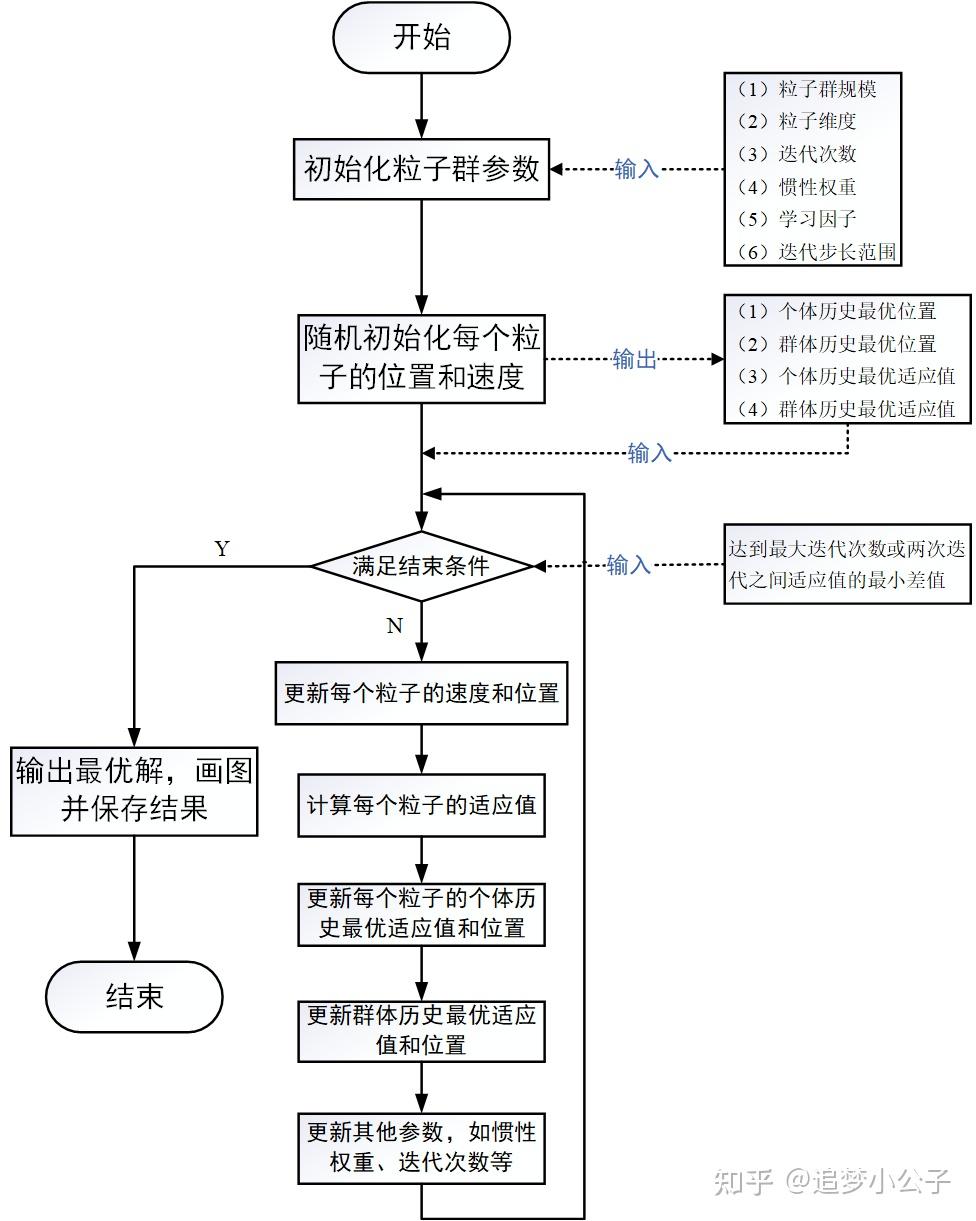
一个正整数，推荐取值范围：[20,1000]，简单问题一般取20~40，较难或特定类别的问题可以取100~200。较小的种群规模容易陷入局部最优；较大的种群规模可以提高收敛性，更快找到全局最优解，但是相应地每次迭代的计算量也会增大；当种群规模增大至一定水平时，再增大将不再有显著的作用。

粒子搜索的空间维数即为自变量的个数。

推荐取值范围：[50,100]，典型取值：60、70、100；这需要在优化的过程中根据实际情况进行调整，迭代次数太小的话解不稳定，太大的话非常耗时，没有必要。

1998年，Yuhui Shi和Russell Eberhart对基本粒子群算法引入了惯性权重(inertia weight) $\\[\\omega\\]$ ，并提出动态调整惯性权重以平衡收敛的全局性和收敛速度，该算法被称为标准PSO算法（本文所介绍）^[2]。

参数意义

惯性权重 $w$ 表示上一代粒子的速度对当代粒子的速度的影响，或者说粒子对当前自身运动状态的信任程度，粒子依据自身的速度进行惯性运动。惯性权重使粒子保持运动的惯性和搜索扩展空间的趋势。 $\\[\\omega\\]$ 值越大，探索新区域的能力越强，全局寻优能力越强，但是局部寻优能力越弱。反之，全局寻优能力越弱，局部寻优能力强。较大的 $\\[\\omega\\]$ 有利于全局搜索，跳出局部极值，不至于陷入局部最优；而较小的 $\\[\\omega\\]$ 有利于局部搜索，让算法快速收敛到最优解。当问题空间较大时，为了在搜索速度和搜索精度之间达到平衡，通常做法是使算法在前期有较高的全局搜索能力以得到合适的种子，而在后期有较高的局部搜索能力以提高收敛精度，所以 $w$ 不宜为一个固定的常数^[3]。

当 $\\[\\omega=1\\]$ 时，退化成基本粒子群算法，当 $\\[\\omega=0\\]$ 时，失去对粒子本身经验的思考。推荐取值范围：[0.4,2]，典型取值：0.9、1.2、1.5、1.8

改善惯性权重 $\\[\\omega\\]$

在解决实际优化问题时，往往希望先采用全局搜索，使搜索空间快速收敛于某一区域，然后采用局部精细搜索以获得高精度的解。因此提出了自适应调整的策略，即随着迭代的进行，线性地减小 $\\[\\omega\\]$ 的值。这里提供一个简单常用的方法——线性变化策略：随着迭代次数的增加，惯性权重 $\\[\\omega\\]$ 不断减小，从而使得粒子群算法在初期具有较强的全局收敛能力，在后期具有较强的局部收敛能力。

$\\[\\omega={{\\omega }_{\\max }}-\\left({{\\omega }_{\\max }}-{{\\omega }_{\\min }}\\right)\\frac{\ ext{iter}}{\ ext{ite}{{\ ext{r}}_{\\max }}}\\\\\\]$

${{\\omega }_{\\max }}$ ——最大惯性权重； ${{\\omega }_{\\min }}$ ——最小惯性权重；

${\ ext{iter}}$ ——当前迭代次数； ${\ ext{ite}{{\ ext{r}}_{\\max }}}$ ——最大迭代次数。

（5）学习因子： ${{c}_{1}},{{c}_{2}}$

也称为加速系数或加速因子（这两个称呼更加形象地表达了这两个系数的作用）

${{c}_{1}}$ 表示粒子下一步动作来源于自身经验部分所占的权重，将粒子推向个体最优位置 $P_{id,pbest}$ 的加速权重；
${{c}_{2}}$ 表示粒子下一步动作来源于其它粒子经验部分所占的权重，将粒子推向群体最优位置 $p_{d\ ext{,gbest}}^{k}$ 的加速权重；
${{c}_{1}}=0$ ：无私型粒子群算法，"只有社会，没有自我"，迅速丧失群体多样性，易陷入局部最优而无法跳出；
${{c}_{2}}=0$ ：自我认知型粒子群算法，"只有自我，没有社会"，完全没有信息的社会共享，导致算法收敛速度缓慢；
${{c}_{1}},{{c}_{2}}$ 都不为0：完全型粒子群算法，更容易保持收敛速度和搜索效果的均衡，是较好的选择。

低的值使粒子在目标区域外徘徊，而高的值导致粒子越过目标区域。推荐取值范围：[0,4]；典型取值： ${{c}_{1}}={{c}_{2}}=2$ 、 ${{c}_{1}=1.6}$ 和 ${{c}_{2}=1.8}$ 、 ${{c}_{1}=1.6}$ 和 ${{c}_{2}=2}$ ，针对不同的问题有不同的取值，一般通过在一个区间内试凑来调整这两个值。

即优化目标函数的值，用来评价粒子位置的好坏程度，决定是否更新粒子个体的历史最优位置和群体的历史最优位置，保证粒子朝着最优解的方向搜索。

限制粒子搜索的空间，即自变量的取值范围，对于无约束问题此处可以省略。

为了平衡算法的探索能力与开发能力，需要设定一个合理的速度范围，限制粒子的最大速度 $v_{max}$ ，即粒子下一步迭代可以移动的最大距离。

$v_{max}$ 较大时，粒子飞行速度快，探索能力强，但粒子容易飞过最优解；
$v_{max}$ 较小时，飞行速度慢，开发能力强，但是收敛速度慢，且容易陷入局部最优解；
$v_{max}$ 一般设为粒子变化范围的10％~20％，可根据实际情况调试，但不能大于粒子(解)的变化范围。

一般有两种：

① 最大迭代步数

② 可接受的满意解：上一次迭代后最优解的适应值与本次迭代后最优解的适应值之差小于某个值后停止优化

粒子群算法优化的结果受很多因素的影响，其中受粒子初始值的影响比较大，而且较难调控。如果粒子初始值是随机初始化的，在不改变任何参数的情况下，多次优化的结果不一定都收敛到一个全局或局部最优解，也可能会得到一个无效解。所以粒子初始化是一个十分重要的步骤，它关系到整个优化过程中优化收敛的速度与方向。如果粒子的初始化范围选择得好的话可以大大缩短优化的收敛时间，也不易于陷入局部最优解。我们需要根据具体的问题进行分析，如果根据我们的经验判断出最优解一定在某个范围内，则就在这个范围内初始化粒子。如果无法确定，则以粒子的取值边界作为初始化范围。

在北理工韩宝玲教授的"基于粒子群算法的四足机器人静步态优化方法^[4]"论文中采用了拉丁方抽样方法来解决粒子初始化问题，大家可以尝试一下这种初始化方法。

这部分等我有空了再补充，个人项目实践代码不方便上传，网上很多采用matlab、python、C语言实现的简单例子，虽然有些符号表示不一致，但是大致意思是一样的。只有跑过代码才能真正地理解算法的内涵，建议复现一下下面的代码：

matlab

最优化算法之粒子群算法（PSO）_青萍之末的博客-CSDN博客粒子群优化算法(PSO)_森的博客-CSDN博客_粒子群算法

python

用python3实现粒子群优化算法（PSO）_FREEMAN-CSDN博客_粒子群优化算法python Python粒子群优化算法实现（PSO）_徐奕的专栏-CSDN博客

我在启发式优化算法讲座上请教过上交大的周杨青老师和港中文的付樟华老师两个问题：

问题1：如何判断是达到了全局最优解还是局部最优解？

回答1：很难确定是达到了全局最优解还是局部最优解的，只能凭感觉......

我在优化的过程中也确实是这样做的，多次优化、观察解的数据和图像，通过感觉判断是否达到了最优解，不管最终结果是不是达到了全局最优解，至少是达到了让我满意的局部最优解。

问题2：如何提高算法的重复精度？在用粒子群算法求解时，并不能保证每次求解都能得到一个较好的解，算法受初始值的影响比较大。

回答2：看算力的，有些初始值会对解影响比较大，有些是没什么影响的。

可能老师们对粒子群算法研究得不多，所以对问题2的回答不是很清晰，如果大家对这两个问题有其他看法可以留言讨论。讲座视频链接：大概在52分15秒的位置

AIRS in the AIR | 运筹优化（二）_哔哩哔哩_bilibili

python中的粒子群算法库、包：pyPSO、scikit-opt、deap

启发式算法库scikit-opt：包括遗传算法(Genetic Algorithm, GA）、粒子群优化(Particle Swarm Optimization, PSO)、模拟退火算法(Simulated Annealing, SA)、蚁群算法(Ant Colony Algorithm, ACA)、免疫算法(Immune Algorithm, IA)、人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)，旅行商问题(Traveling Salesman Problem, TSP ）。
优化算法库deap：包括遗传算法、粒子群优化等。

另外，笔者发表了一篇采用PSO算法优化四足机器人足端轨迹的小论文，感兴趣的朋友可以去瞅瞅：

Biologically Inspired Planning and Optimization of Foot Trajectory of a Quadruped Robot

[1]Kennedy J . Particle swarm optimization[J]. Proc. of 1995 IEEE Int. Conf. Neural Networks, (Perth, Australia), Nov. 27-Dec. 2011, 4(8):1942-1948 vol.4.
[2]Shi Y . A Modified Particle Swarm Optimizer[C]// Proc of IEEE Icec Conference. 1998.
[3]Y. Shi and R. C. Eberhart. Empirical study of particle swarm optimization. Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 1999, pp. 1945-1950 Vol. 3.
[4]Eberhart R C , Shi Y . Comparison between genetic algorithms and particle swarm optimization[C]// Evolutionary Programming VII, 7th International Conference, EP98, San Diego, CA, USA, March 25-27, 1998, Proceedings. Springer, Berlin, Heidelberg, 1998.
[5]Eberhart, Shi Y . Particle swarm optimization: developments, applications and resources[C]// Congress on Evolutionary Computation. IEEE, 2002.
[6]Clerc M , Kennedy J . The particle swarm - explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1):58-73.
[7]Trelea I C . The particle swarm optimization algorithm: Convergence analysis and parameter selection[J]. Information Processing Letters, 2003, 85( 6):317-325.
[8]杨维,李歧强. 粒子群优化算法综述[J]. 中国工程科学, 6(5):87-94.
[9]王俊伟, 汪定伟. 粒子群算法中惯性权重的实验与分析[J]. 系统工程学报, 2005, 20(2):194-198.
[10]黄少荣. 粒子群优化算法综述[J]. 计算机工程与设计, 2009(08):1977-1980.
[11]王杰文, 李赫男. 粒子群优化算法综述[J]. 现代计算机(专业版), 2009, 30(002):22-27.
[12]周俊,陈璟华,刘国祥, 等.粒子群优化算法中惯性权重综述[J].广东电力,2013,26(7):6-12.
[13]杨博雯, 钱伟懿. 粒子群优化算法中惯性权重改进策略综述[J]. 渤海大学学报(自然科学版), 2019, v.40;No.121(03):86-100.
[14]北京交通大学高士根、王悉教授的《人工智能基础及应用》课程

写于2021.1.22......

上一篇：图像优化意味着什么？图片优化有什么用？如何做图片优化？

下一篇：拆解报告：SolarEdge嵌入式330W光伏功率优化器OPJ300-LV

粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读

友情链接：